1 5 Odds Meaning

American odds are primarily used by sites that cater to US sports bettors, also know as “moneyline odds” they are the odds most often used for moneyline betting for American sports bettors. American odds are probably the easiest to understand as odds represent how much the bettor will have to wager to win $100.

1. A fractional listing of 6/1 (six-to-one) odds would mean that you win $6 against every $1 you wager (in addition to receiving your dollar back, i.e. $1 – the amount you wagered).
2. ((£10/2) x 5) + £10) = £35. For longer odds with a larger return, look out for odds where the first half of the fraction is larger than the second half. For example: Odds of 5/1 will return greater winnings than odds of 1/5. If you were to stake £10 on odds of 5/1, then your return would be £60.

1-4 runners: win only. 5-7 runners: 1/4 odds a place for 1,2. 8+ runners: 1/5 odds a place for 1,2,3. 12-15 runners in handicaps only: 1/4 odds a place 1,2,3; 16+ runners in handicaps only: 1/4 odds a place 1,2,3,4. The place terms in other sporting events will be advertised on the event in question, but do generally follow the pattern above.

Introduction

American Odds are simply one way to express odds. A pick em will be listed as “pk” or “pick” or “pick ’em” depending on your site. There are two basic types, favorites and underdogs

Favorites come with a – symbol attached. The higher the absolute value of the number, the better the chance the bet will win. So for example a -200 favorite has a better chance to win than a -120 favorite. 200 is greater than 120 so this is what we mean by absolute value, you ignore the – sign and take just the number when considering this.

Underdogs come with a + symbol attached. The higher the number, the larger the underdog. So a +200 underdog has a better chance to win than a +500 underdog.

Have a look at the betting markets at some of our highest-rated bookmakers to see how they price up games in American odds:

Terms & Conditions: T&Cs Apply. Full terms apply.

What Do The Odds Mean?

American Odds always use a baseline value of $100. For favorites you are always risking the money to win $100, and with underdogs you risk $100 to win the amount.

A -135 favorite means you must risk $135 to win $100 from the sports book. So you either lose $135 or win $100, or push.

A +350 underdog means you risk only $100, but you win $350. You either lose $100 or win $350, or push.

American Odds can easily be converted into other odds such as decimal or fraction, using our free online calculator. Most, if not all, sites also offer odds in those formats, by simply choosing your preferred format.

We can also convert American Odds into percentages. This is useful because it gives you a breakeven % that you need to achieve long-term to win when betting certain odds.

The most common odds are -110 so we will use that. The question to ask is “how often will we need to win, when betting at -110 odds, to break even?” The answer is “enough so that you turn 110 into 210 often enough to overcome the juice” but it is expressed in percentages. So we take our $110 risked, divided by the ultimate $210 payout if our ticket cashes, and come up with .5238 or 52.38%. This means you must win at least 52.38% of your bets at -110 to break even.

Another example will involve underdogs. Let’s say we have a +200 underdog. How often do they have to win for us to break even? We take a $100 risk and divide by the ultimate payout of $300 and get .3333, or 33.33%. So any +200 underdog that wins 34%+ of the time is a profitable bet.

1 5 Odds Meaning Math

American odds are attached to point spreads in most American sports such as the NFL and NBA. Here is an example from the NFL:

Atlanta +3 -115
Carolina -3 +110

The American odds will give the bookmaker influence over the point spread without changing the key number of 3. Odds worse than -110 as we discussed can hurt your breakeven percentage and should be taken into account even when betting spreads. On the other hand, underdog plus odds will help your bottom line.

Conclusion

American Odds are convenient and fast once you get accustomed to them. Just like any other format, it is all personal preference. It is also easy to convert American Odds to fractional or decimal odds and can easily be done using our online odds converter.

Ready For More?

Odds and odds ratios are an important measure of the absolute/relative chance of an event of interest happening, but their interpretation is sometimes a little tricky to master. In this short post, I’ll describe these concepts in a (hopefully) clear way.

From probability to odds

Our starting point is that of using probability to express the chance that an event of interest occurs. So a probability of 0.1, or 10% risk, means that there is a 1 in 10 chance of the event occurring. The usual way of thinking about probability is that if we could repeat the experiment or process under consideration a large number of times, the fraction of experiments where the event occurs should be close to the probability (e.g. 0.1).

The odds of an event of interest occurring is defined by odds = p/(1-p) where p is the probability of the event occurring. So if p=0.1, the odds are equal to 0.1/0.9=0.111 (recurring). So here the probability (0.1) and the odds (0.111) are quite similar. Indeed whenever p is small, the probability and odds will be similar. This is because when p is small, 1-p is approximately 1, so that p/(1-p) is approximately equal to p.

But when p is not small, the probability and odds will generally be quite different. For example if p=0.5, we have odds=0.5/0.5=1. As p increases, the odds get larger and larger. For example, with p=0.99, odds=0.99/0.01=99.

Fractional odds and gambling

Particularly in the world of gambling, odds are sometimes expressed as fractions, in order to ease mental calculations. For example, odds of 9 to 1 against, said as “nine to one against”, and written as 9/1 or 9:1, means the event of interest will occur once for every 9 times that the event does not occur. That is in 10 times/replications, we expect the event of interest to happen once and the event not to happen in the other 9 times. Using odds to express probabilities is useful in a gambling setting because it readily allows one to calculate how much one would win – with odds of 9/1 you will win 9 for a bet of 1 (assuming your bet comes good!).

1 5 Odds Meaning Dictionary

Odds ratios

In the statistics world odds ratios are frequently used to express the relative chance of an event happening under two different conditions. For example, in the context of a clinical trial comparing an existing treatment to a new treatment, we may compare the odds of experiencing a bad outcome if a patient takes the new treatment to the odds of a experiencing a bad outcome if a patient takes the existing treatment.

Suppose that the probability of a bad outcome is 0.2 if a patient takes the existing treatment, but that this is reduced to 0.1 if they take the new treatment. The odds of a bad outcome with the existing treatment is 0.2/0.8=0.25, while the odds on the new treatment are 0.1/0.9=0.111 (recurring). The odds ratio comparing the new treatment to the old treatment is then simply the correspond ratio of odds: (0.1/0.9) / (0.2/0.8) = 0.111 / 0.25 = 0.444 (recurring). This means that the odds of a bad outcome if a patient takes the new treatment are 0.444 that of the odds of a bad outcome if they take the existing treatment. The odds (and hence probability) of a bad outcome are reduced by taking the new treatment. We could also express the reduction by saying that the odds are reduced by approximately 56%, since the odds are reduced by a factor of 0.444.

1 5 Odds Meaning Against

Why odds ratios, and not risk/probability ratios?

People often (I think quite understandably) find odds, and consequently also an odds ratio, difficult to intuitively interpret. An alternative is to calculate risk or probability ratios. In the clinical trial example, the risk (read probability) ratio is simply the ratio of the probability of a bad outcome under the new treatment to the probability under the existing treatment, i.e. 0.1/0.2=0.5. This means the risk of a bad outcome with the new treatment is half that under the existing treatment, or alternatively the risk is reduced by a half. Intuitively the risk ratio is much easier to understand. So why do we use odds and odds ratios in statistics?

Logistic regression

Often we want to do more than just compare two groups in terms of the probability/risk/odds of an outcome. Specifically, we often are interested in fitting statistical models which describe how the chance of the event of interest occurring depends on a number of covariates or predictors. Such models can be fitted within the generalized linear model family. The most popular model is logistic regression, which uses the logit link function. This choice of link function means that the fitted model parameters are log odds ratios, which in software are usually exponentiated and reported as odds ratios. The logit link function is used because for a binary outcome it is the so called canonical link function, which without going into further details, means it has certain favourable properties. Consequently when fitting models for binary outcomes, if we use the default approach of logistic regression, the parameters we estimate are odds ratios.

An alternative to logistic regression is to use a log link regression model, which results in (log) risk ratio parameters. Unfortunately historically these have suffered from numerical issues when attempting to fit them to data (see here for a paper on this). However there is also a more fundamental issue with log link regression, in that the log link means that certain combinations of covariate values can lead to fitted probabilities outside of the (0,1) range.

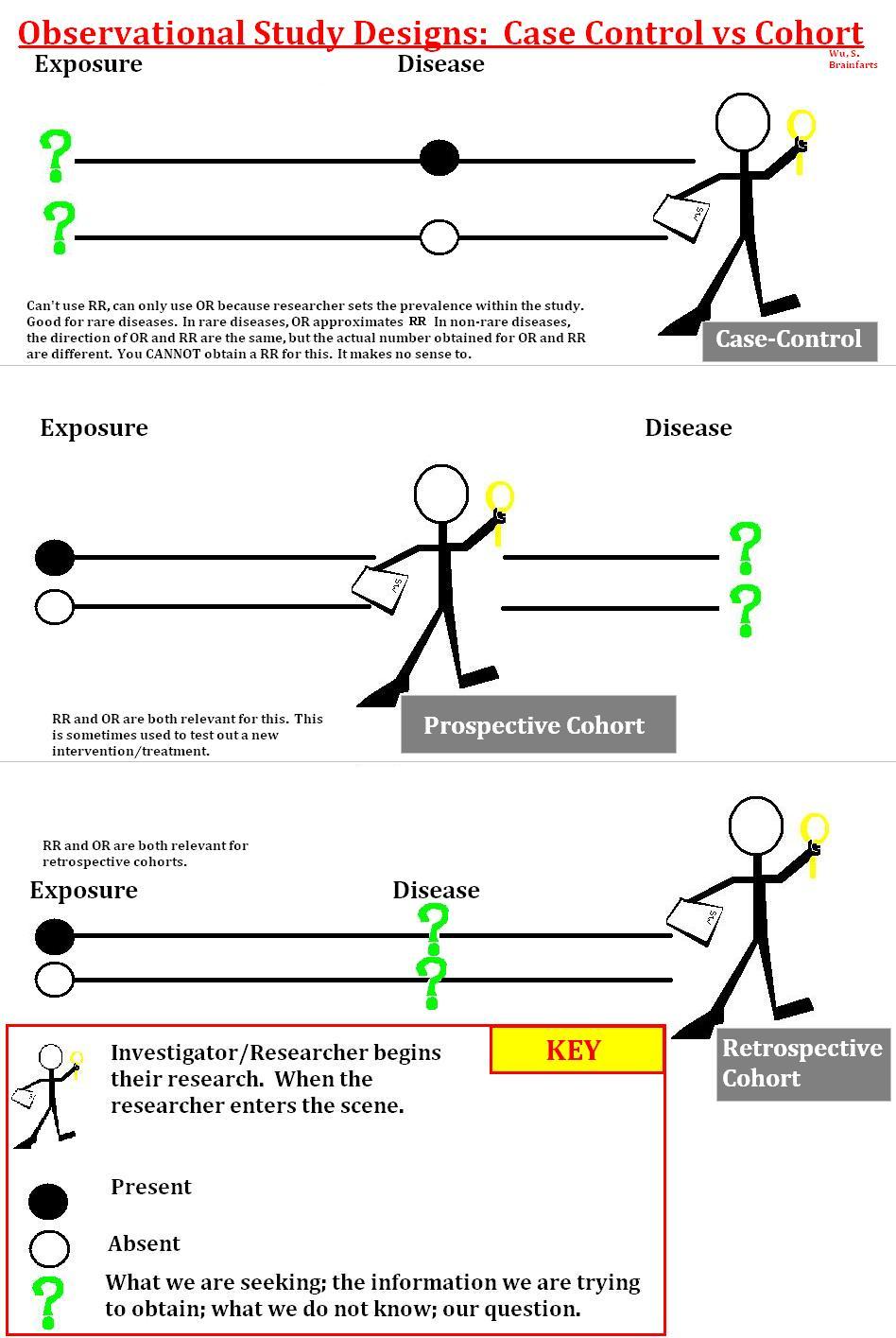
Case control studies

In case control studies individuals are selected into the study with a probability which depends on whether they experienced the event of interest or not. They are particularly useful for studying diseases which occur rarely. A case control study might (attempt to) enroll all those who experience the event of interest in a given period of time, along with a number of ‘controls’, i.e. individuals who did not experience the event of interest. In a case control study the proportion of cases is under the investigator’s control, and in particular the proportion in the study is not representative of the incidence in the target population. As a consequence, one cannot estimate risk or risk ratios from case control studies, at least not without external additional information. However, it turns out that the odds ratio can still be validly estimated with a case control design, due to a certain symmetry property possessed by the odds ratio.

Rare outcomes

When the event of interest is rare (i.e. the probability of it occurring is low), the odds and risk ratios are numerically quite similar. Thus in situations with rare outcomes an odds ratio can be interpreted as if it were a risk ratio, since they will be numerically similar. However, when the outcome is not rare, the two measures can be substantially different (see here, for example).