Odds To Probability Formula
- Formula To Convert Probability To Odds
- Odds To Probability Formula Solver
- How To Calculate Odds
- How To Write Odds
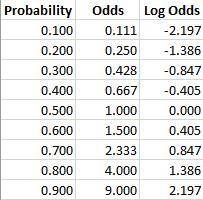
- Finding Odds using Probability Probabilities for and against the event can be used as the antecedent and consequent of the ratio representing the odds for an event in place of favorable and unfavorable choices.
- There was a total of three wins out of five, so the probability of winning this year is 3/5 = 0.6 = 60%. Expressed in terms of odds, we have that there were three wins for the Quakers and two losses, so the odds in favor of them winning are 3:2.
- Odds: the ratio of the probability that an event will occur versus the probability that the event will not occur, or probability / (1-probability). For example, if you are normally on call 2 out of 7 days in a week, then the odds of you being on call on a certain day of the week is (2/7)/(5/7) = 0.40.
We often use the odds ratio and relative risk when performing an analysis on a 2-by-2 table, which takes on the following format:
The odds ratio tells us the ratio of the odds of an event occurring in a treatment group to the odds of an event occurring in a control group. It is calculated as:
Odds ratio = (A*D) / (B*C)

The relative risk tells us the ratio of the probability of an event occurring in a treatment group to the probability of an event occurring in a control group. It is calculated as:

Labs(title ='probability versus odds') 0.00 0.25 0.50 0.75 1.00 0 50 100 150 odds p probability versus odds Finally, this is the plot that I think you’llfind most useful because inlogistic regression yourregression. Calculate the probability of winning according to the odds formulas: 5/17 = 29.41%. Calculate the probability of losing according to the odds formulas: 12/17 = 70.59%. Check whether the result is correct with the betting odds calculator.
Relative risk = [A/(A+B)] / [C/(C+D)]
This tutorial explains how to calculate odds ratios and relative risk in Excel.
How to Calculate the Odds Ratio and Relative Risk
Suppose 50 basketball players use a new training program and 50 players use an old training program. At the end of the program we test each player to see if they pass a certain skills test. The following table shows the number of players who passed and failed, based on the program they used:
The odds ratio is calculated as (34*11) / (16*39) = 0.599
We would interpret this to mean that the odds that a player passes the test by using the new program are just 0.599 times the odds that a player passes the test by using the old program. In other words, the odds that a player passes the test are actually lowered by 40.1% by using the new program.
The relative risk is calculated as [34/(34+16)] / [39/(39+11)] = 0.872
We would interpret this to mean that the ratio of the probability of a player passing the test using the new program compared to the old program is 0.872. Because this value is less than 1, it indicates that the probability of passing is actually lower under the new program compared to the old program.
We could also see this by directly computing the probability that a player passes under each program:
Probability of passing under new program = 34 / 50 = 68%
Probability of passing under old program = 39 / 50 = 78%
How to Calculate Confidence Intervals
Once we calculate the odds ratio and relative risk, we may also be interested in computing confidence intervals for these two metrics.
A 95% confidence interval for the odds ratio can be calculated using the following formula:
95% C.I. for odds ratio = exp(ln(OR) – 1.96*SE(ln(OR))) to exp(ln(OR) – 1.96*SE(ln(OR)))
where SE(ln(OR)) =√1/A + 1/B + 1/C + 1/D
The 95% C.I. for the odds ratio turns out to be (.245, 1.467). The image below shows the formula we used to calculate this confidence interval:

Formula To Convert Probability To Odds
A 95% confidence interval for the relative risk can be calculated using the following formula:
Odds To Probability Formula Solver
95% C.I. for relative risk = exp(ln(RR) – 1.96*SE(ln(RR))) to exp(ln(RR) – 1.96*SE(ln(RR)))
How To Calculate Odds
where SE(ln(RR)) =√1/A + 1/C – 1/(A+B) – 1/(C+D)
How To Write Odds
The 95% C.I. for the relative risk turns out to be (.685, 1.109). The image below shows the formula we used to calculate this confidence interval: